Notes

• 配列のサイズ変更
• データ構造
• 連結リスト
• 配列の実装
• 連結リストの実装
• 木構造
• その他のデータ構造

配列のサイズ変更

• 前回は、ポインタやmallocなど、メモリを操作するための便利なツールについて学びました。

• Week2では、同じ種類の値をリストにしてメモリ上に連続して格納できる「配列」について学びました。要素を挿入する必要がある場合は、配列のサイズも大きくする必要があります。しかし、コンピュータの次のメモリは、文字列などの他のデータに既に使用されている可能性があります。

1つの解決策は、十分なスペースがある場所により多くのメモリを割り当て、そこに配列を移動することです。ただし、最初に元のn個の要素をそれぞれコピーする必要があるため、配列をそこにコピーする必要があります。これは、実行時間がO（n）の操作になります。

• 配列に要素を挿入する際の下限はΩ(1)となります。これは配列の中にすでに要素を入れるスペースがあるかもしれないからです。

データ構造

• データ構造は、メモリ内のデータを編成するためのより複雑な方法であり、さまざまなレイアウトで情報を格納できます。
• データ構造を構築するには、いくつかのツールが必要です。
  • struct （構造体）を使って独自のデータ型を作成する
  • .で構造内のプロパティへアクセスする
  • *でポインタが指すメモリ内のアドレスに移動する
  • ->でポインタが指す構造体のプロパティにアクセスする

連結リスト

• 連結リストを使用すると、値をメモリの異なる部分に格納することで簡単に拡張できる値のリストを格納できます。

• 値1, 2, 3があり、それぞれ0x123, 0x456, 0x789のようなメモリ上のアドレスにあります。
  • 値がメモリ内で隣り合っていないため、配列とは異なります。メモリ内の空いている任意の場所を使用できます。

• これらの値をすべて追跡するには、格納する値と次の要素のアドレスの両方に十分なメモリを各要素に割り当てることによって、リストをリンクする必要があります。

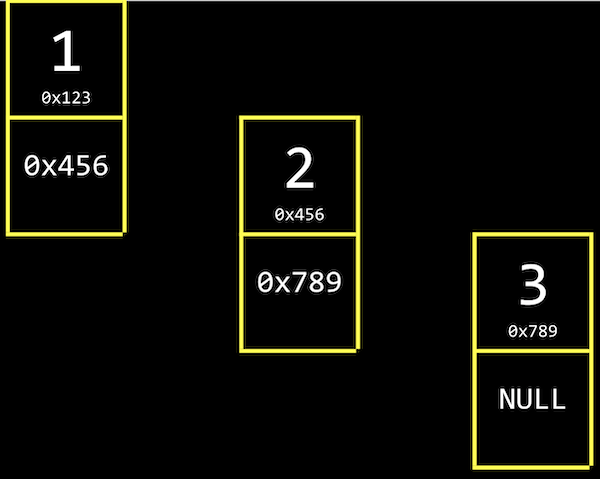
• たとえば、値1の次に、次の値へのポインタ0x456も格納します。これを、値とポインタの両方を格納するデータ構造のコンポーネントであるノードと呼びます。Cでは、構造体を使ってノードを実装します。
  • 値が3の最後のノードには、次の要素がないため、NULLポインタがあります。別のノードを挿入する必要がある場合は、その単一のNULLポインタを新しい値を指すように変更するだけです。
• 値の追加に費やす時間を少なくする代わりに、各要素に2倍のメモリを割り当てる必要があるというトレードオフがあります。ノードがメモリ内のどこにあってもよいため、二分探索は使用できません。これらにアクセスするには、ポインタを1つずつたどるしかありません。
• コードでは、nodeという構造体を作成し、int 型のnumber、そしてnextという次のノードへのポインタの両方の値を格納する必要があります。

typedef struct node
{
    int number;
    struct node *next;
}
node;

• この構造体をtypedef struct nodeで始めて、構造体内のノードを参照できるようにします。
• 連結リストは、structから始まるコードで作成できます。まず、空のリストを準備するため、NULLポインタnode *list = NULL;を使用します。
• 要素を追加するには、まずノードにメモリを割り当て、その値を設定する必要があります。

// We use sizeof(node) to get the right amount of memory to allocate, and
// malloc returns a pointer that we save as n
node *n = malloc(sizeof(node));

// We want to make sure malloc succeeded in getting memory for us
if (n != NULL)
{
    // This is equivalent to (*n).number, where we first go to the node pointed
    // to by n, and then set the number property. In C, we can also use this
    // arrow notation
    n->number = 1;
    // Then we need to make sure the pointer to the next node in our list
    // isn't a garbage value, but the new node won't point to anything (for now)
    n->next = NULL;
}

• ここで、リストはノードlist = n;を指す必要があります。

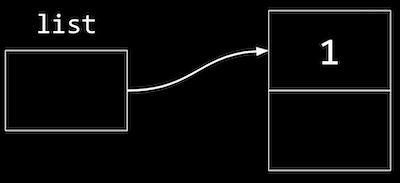
• リストに追加するには、同じ方法でメモリを追加して新しいノードを作成します。

n = malloc(sizeof(node));
if (n != NULL)
{
    n->number = 2;
    n->next = NULL;
}

• しかしここで、最初のノードのポインタを新しいnを指すように更新する必要があります。

list->next = n;

• 3番目のノードを追加する場合も同様にして、最初にリスト内のnextポインタをたどっていき、nextポインタで新しいノードを指すように設定します。

n = malloc(sizeof(node));
if (n != NULL)
{
    n->number = 3;
    n->next = NULL;
}
list->next->next = n;

• メモリ内のノードは次のように表示されます。

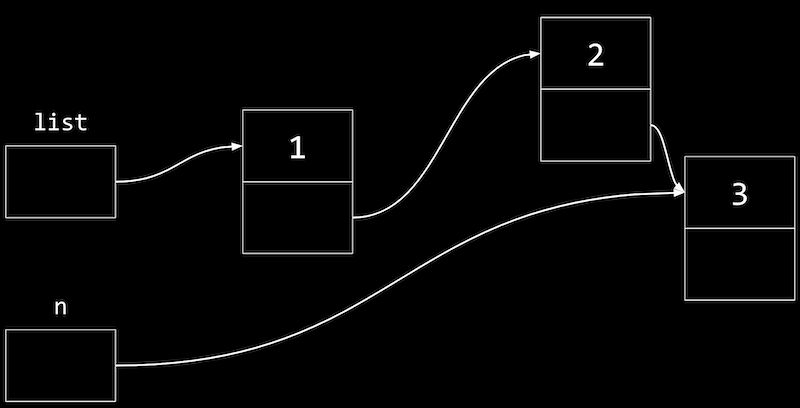
• nは一時変数で、値3の新しいノードを指します。
  • 値2のノードのポインタも新しいノードを指すようにしたいので、list (値1のノードを指す) から始め、nextポインタを辿って値2のノードに移動し、nextポインタをnを指すように更新します。
• その結果、連結リストの検索にもO(n)の実行時間がかかります。これは、リストがソートされている場合でも、各ポインタに従ってすべての要素を順番に調べる必要があるためです。リストの先頭に新しいノードを挿入すると、連結リストへの挿入の実行時間はO(1)になります。

配列の実装

• 配列のサイズ変更を実装する方法を見てみましょう。

#include <stdio.h>
#include <stdlib.h>

int main(void)
{
    // Use malloc to allocate enough space for an array with 3 integers
    int *list = malloc(3 * sizeof(int));
    if (list == NULL)
    {
        return 1;
    }

    // Set the values in our array
    list[0] = 1;
    list[1] = 2;
    list[2] = 3;

    // Now if we want to store another value, we can allocate more memory
    int *tmp = malloc(4 * sizeof(int));
    if (tmp == NULL)
    {
        free(list);
        return 1;
    }

    // Copy list of size 3 into list of size 4
    for (int i = 0; i < 3; i++)
    {
        tmp[i] = list[i];
    }

    // Add new number to list of size 4
    tmp[3] = 4;

    // Free original list of size 3
    free(list);

    // Remember new list of size 4
    list = tmp;

    // Print list
    for (int i = 0; i < 4; i++)
    {
        printf("%i\n", list[i]);
    }

    // Free new list
    free(list);
}

• malloc はメモリを割り当て、ヒープ領域から解放することを思い出してください。別のライブラリ関数reallocを呼び出して、以前に割り当てたメモリを再割り当てすることができます。

int *tmp = realloc(list, 4 * sizeof(int));

• そしてrealloc は古い配列listを、渡したサイズのより大きなメモリ領域にコピーします。既存のメモリチャンクの後にスペースがある場合、同じアドレスが返されますが、その後のメモリも変数に割り当てられます。

連結リストの実装

• 以前のコードの断片を、連結リストを実装するプログラムに結合してみましょう。

#include <stdio.h>
#include <stdlib.h>

// Represents a node
typedef struct node
{
    int number;
    struct node *next;
}
node;

int main(void)
{
    // List of size 0. We initialize the value to NULL explicitly, so there's
    // no garbage value for our list variable
    node *list = NULL;

    // Allocate memory for a node, n
    node *n = malloc(sizeof(node));
    if (n == NULL)
    {
        return 1;
    }

    // Set the value and pointer in our node
    n->number = 1;
    n->next = NULL;

    // Add node n by pointing list to it, since we only have one node so far
    list = n;

    // Allocate memory for another node, and we can reuse our variable n to
    // point to it, since list points to the first node already
    n = malloc(sizeof(node));
    if (n == NULL)
    {
        free(list);
        return 1;
    }

    // Set the values in our new node
    n->number = 2;
    n->next = NULL;

    // Update the pointer in our first node to point to the second node
    list->next = n;

    // Allocate memory for a third node
    n = malloc(sizeof(node));
    if (n == NULL)
    {
        // Free both of our other nodes
        free(list->next);
        free(list);
        return 1;
    }
    n->number = 3;
    n->next = NULL;

    // Follow the next pointer of the list to the second node, and update
    // the next pointer there to point to n
    list->next->next = n;

    // Print list using a loop, by using a temporary variable, tmp, to point
    // to list, the first node. Then, every time we go over the loop, we use
    // tmp = tmp->next to update our temporary pointer to the next node. We
    // keep going as long as tmp points to somewhere, stopping when we get to
    // the last node and tmp->next is null.
    for (node *tmp = list; tmp != NULL; tmp = tmp->next)
    {
        printf("%i\n", tmp->number);
    }

    // Free list, by using a while loop and a temporary variable to point
    // to the next node before freeing the current one
    while (list != NULL)
    {
        // We point to the next node first
        node *tmp = list->next;
        // Then, we can free the first node
        free(list);
        // Now we can set the list to point to the next node
        list = tmp;
        // If list is null, when there are no nodes left, our while loop will stop
    }
}

• 連結リストの先頭にノードを挿入する場合は、リスト変数を更新する前に、ノードが後続ノードを指すように慎重に更新する必要があります。そうしないと、リストの残りの部分が失われます。

// Here, we're inserting a node into the front of the list, so we want its
// next pointer to point to the original list. Then we can change the list to
// point to n.
n->next = list;
list = n;

• 最初に、値1のノードがリストの先頭を指し、値2のノードがあります。

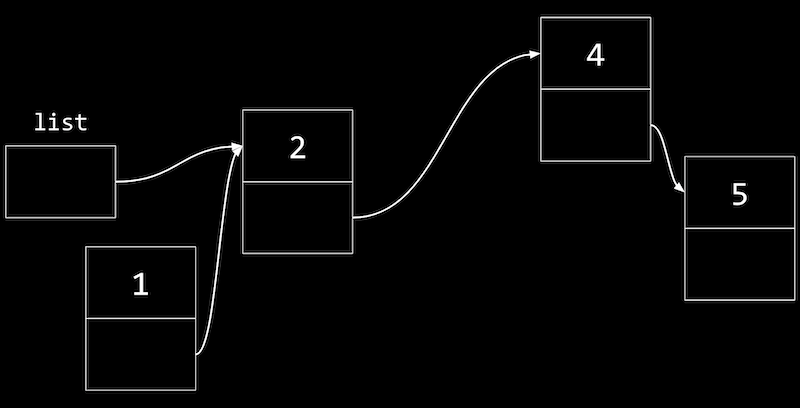
• 変数listを更新して、値1のノードを指すようにし、リストの残りの部分を失わないようにします。
• 同様に、リストの途中にノードを挿入するには、まず新しいノードのnextポインタを挿入する位置の次のノードを指すように変更します。次に前のノードのnextポインタを更新して新しいノードを指すようにします。
• 連結リストは、ポインタを使用して柔軟なデータ構造をメモリ内に構築する方法を示していますが、これは1次元でしか可視化できません。

木構造

• ソートされた配列では、二分探索を使って要素を探すことができます。まず真ん中（黄色）から始めて、次にどちらかの半分の真ん中（赤）、最後に必要に応じて左か右（緑）を探します。

• 配列を使用すると、配列の任意のインデックスを使って要素を参照するため、O(1)回で要素にランダムにアクセスできます。
• ツリーは別のデータ構造であり、各ノードは左 (値が小さい) と右 (値が大きい) の2つの他のノードを指します。

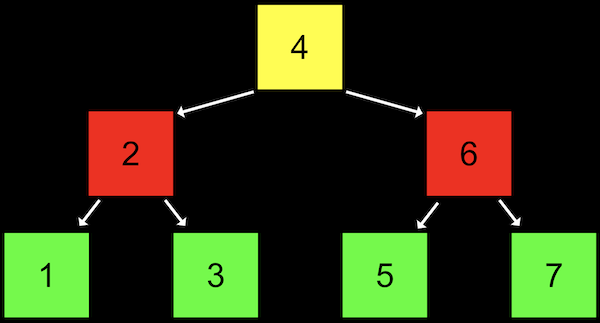
• このデータ構造を2次元で視覚化したことに注目してください (メモリ内のノードは任意の場所に配置できます) 。
  • これは、各ノードが他のノードへのポインタを1つではなく2つ持っている、連結リスト内のノードのより複雑なバージョンで実装できます。ノードの左側の値はすべて小さく、右側のノードの値はすべて大きいため、これを二分探索木として使用できます。データ構造自体は再帰的に定義されるため、再帰関数を使用してデータ構造を操作できます。
  • 各ノードには最大で2つの子ノード、つまりノードが指すノードがあります。
  • 連結リストと同様に、リストの先頭へのポインタを保持しますが、この場合はルート、つまりツリーの最上部の中央ノード (4) をポイントします。
• 1つではなく2つのポインタを持つノードを定義できます。

typedef struct node
{
    int number;
    struct node *left;
    struct node *right;
}
node;

• ツリーを再帰的に検索する関数を作成します。

// tree is a pointer to a node that is the root of the tree we're searching in.
// number is the value we're trying to find in the tree.
bool search(node *tree, int number)
{
    // First, we make sure that the tree isn't NULL, if we've reached a node
    // on the bottom, or if our tree is entirely empty
    if (tree == NULL)
    {
        return false;
    }
    // If we're looking for a number that's less than the tree's number,
    // search the left side, using the node on the left as the new root
    else if (number < tree->number)
    {
        return search(tree->left, number);
    }
    // Otherwise, search the right side, using the node on the right as the new root
    else if (number > tree->number)
    {
        return search(tree->right, number);
    }
    // Finally, we've found the number we're looking for, so we can return true.
    // We can simplify this to just "else", since there's no other case possible
    else if (number == tree->number)
    {
        return true;
    }
}

• 二分探索木では、各ノードが値と2つのポインタ用のスペースを必要とするため、さらに多くのメモリが必要になります。新しい値を挿入するには、間に入るべきノードを見つける必要があるため、O(log n)の時間がかかります。

• しかし、十分な数のノードを追加すると、検索ツリーが連結リストのように見えるようになる可能性があります。

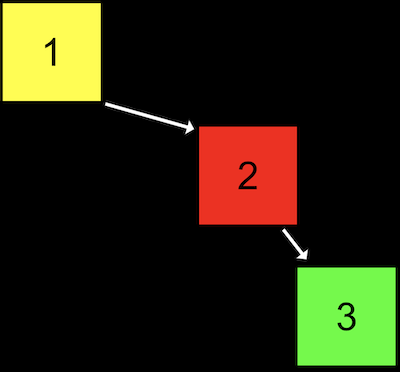
• 値が1のノードから開始し、値が2のノードを追加し、最後に値が3のノードを追加しました。このツリーは二分探索木の制約には従っていますが、それほど効率的ではありません。
  • 値が2のノードを新しいルートノードにすることで、ツリーをバランスの取れた最適な状態にすることができます。より高度なコースでは、ノードが追加されたときにツリーのバランスを保つのに役立つデータ構造とアルゴリズムを扱います。

その他のデータ構造

• ほぼ一定の時間O(1)で探索ができるデータ構造はハッシュテーブルであり、連結リストの配列が元になっています。配列内の各連結リストには、特定のカテゴリの要素があります。

• たとえば、多数の名前があり、アルファベットの文字ごとに1つずつ、26個の位置を持つ配列にソートするとします。

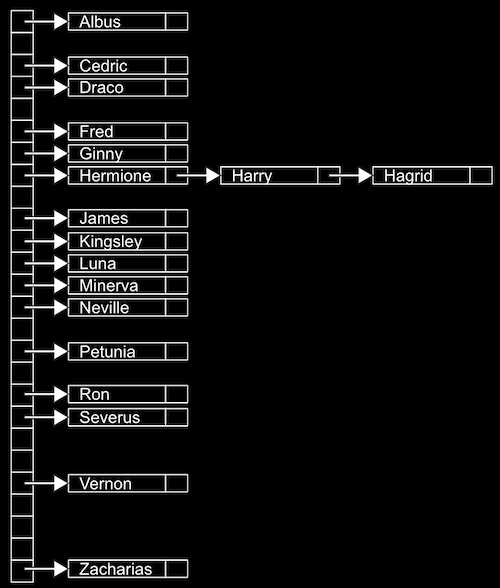
• 配列へのランダムアクセスが可能なので、配列内の位置 (バケット) に要素とインデックスをすばやく設定できます。
• ロケーションには複数の一致する値がある場合がありますが、Hermione、Harry、およびHagridの例でみられるように、連結リスト内のノードであるため、別の値として値を追加できます。配列のサイズを大きくしたり、他の値を移動したりする必要はありません。
• これはハッシュ関数を使用しているため、ハッシュテーブルと呼ばれます。ハッシュ関数は入力を受け取り、入力されるべき場所に確定的にマップします。この例では、ハッシュ関数は単に名前の最初の文字に対応するインデックスを返します。たとえば、 「Albus」 の場合は0、 「Zacharias」 の場合は25を返します。

• しかし、最悪の場合、すべての名前が同じ文字で始まる可能性があるため、再び単一の連結リストに相当するものになる可能性があります。最初の2文字を見て、26*26のハッシュ値、または26*26*26のハッシュ値を必要とする最初の3文字に十分なバケットを割り当てることができます。

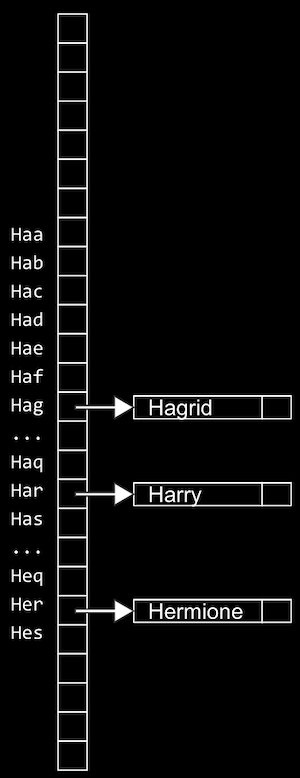
• これらのバケットの一部が空になるため、メモリの使用容量が増えますが、値を検索するために必要な手順は1つだけになり、検索の実行時間が短縮されます。
• 一般的なトランプカードを整理するには、まずスペード、ダイアモンド、ハート、クラブを絵柄ごとに分けて積み重ねることから始めます。そうすれば、それぞれの山をもう少し早く分類することができます。
• nが非常に大きくなると、たとえ数百または数千のバケットがあったとしても、各バケットはnのオーダーの値を持つため、ハッシュテーブルの最悪のケースの実行時間はO(n)であることが判明します。しかし、実際には、値を複数のバケットに分割しているため、実行時間が短縮されます。
• Problem set5では、データ構造内の値を検索する実世界の実行時間を改善し、メモリの使用量のバランスを取ることが課題となります。

• trie (「try」 のように発音され、 「retrieval」 の省略形) と呼ばれる別のデータ構造を使用することもできます。trieは、配列をノードとするツリーです。

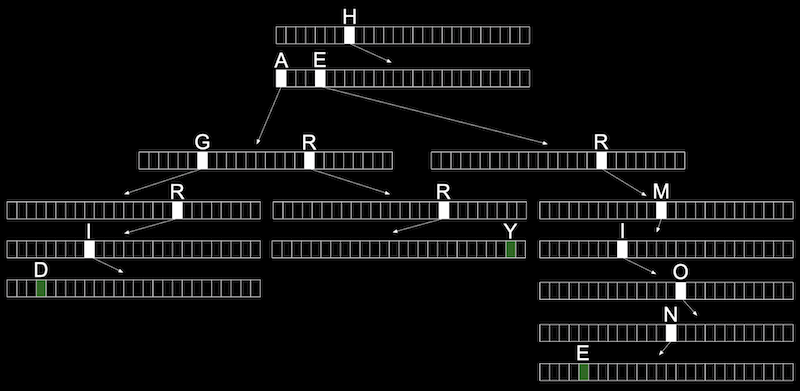
• 各配列には、それぞれの文字A~Zが格納されます。各単語について、最初の文字は配列を指し、次の有効な文字は別の配列を指すというように、有効な単語の終わりを示すブール値 (上の緑色のマーク付き) に達するまで続きます。単語がtrieに含まれていない場合、いずれの配列にも単語のポインタや終了文字を含みません。
  • 上記のtrieには、Hagrid、Harry、Harmioneいう単語があります。
  • データ構造に多くの単語が含まれている場合でも、最大検索時間は探している単語の長さになります。これは固定された最大値とみなせるため、検索と挿入にO(1)を使用できます。
  • このためのコストは、ポインタとブール値を有効な単語のインジケータとして保存するために大量のメモリを必要とすることです。
• さらに高レベルの構造、抽象的なデータ構造があり、配列、連結リスト、ハッシュテーブル、trieの構成要素を使用して、何らかの問題に対する解決策を実装します。
• たとえば、1つの抽象データ構造は、人が列に並んでいるような待ち行列で、最初に入力した値が最初に取り出される値、つまり先入れ先出し (FIFO) になります。値を追加するにはエンキューし、値を取り出すにはデキューします。このデータ構造は抽象的です。なぜなら、これはさまざまな方法で実装できるという考えからです。項目を追加したり取り出したりするときにサイズを変更する配列を使用したり、値を末尾に追加する連結リストを使用したりします。
• 反対のデータ構造はスタックで、最後に追加された項目が最初に取り出されます (後入れ先出し 、LIFO) 。衣料品店では、1番上にあるセーターをスタックから取り出し (pop) 、新しいセーターも最上位に追加 (push) されます。
• 抽象データ構造のもう1つの例として、辞書があります。辞書では、キーを値にマップできます。たとえば、単語を値の定義にマップできます。時間と空間のトレードオフを考慮して、ハッシュテーブルまたは配列を使用して実装できます。
• これらのデータ構造に関するアニメーション 「Jack Learns the Facts About Queues and Stacks」 を見てみましょう。