次のように、Tideman選挙を実行するプログラムを実装します。
./tideman Alice Bob Charlie
Number of voters: 5
Rank 1: Alice
Rank 2: Charlie
Rank 3: Bob
Rank 1: Alice
Rank 2: Charlie
Rank 3: Bob
Rank 1: Bob
Rank 2: Charlie
Rank 3: Alice
Rank 1: Bob
Rank 2: Charlie
Rank 3: Alice
Rank 1: Charlie
Rank 2: Alice
Rank 3: Bob
Charlie
背景
選挙の勝者を決定するための非常に単純なアルゴリズムである多数決選挙については、すでにご存知でしょう。すべての投票者が1票を獲得し、最も多くの票を持つ候補者が勝利します。
しかし、多数決にはいくつかの欠点があります。例えば、3人の候補者がいて下の投票が行われる選挙ではどうなるでしょうか?
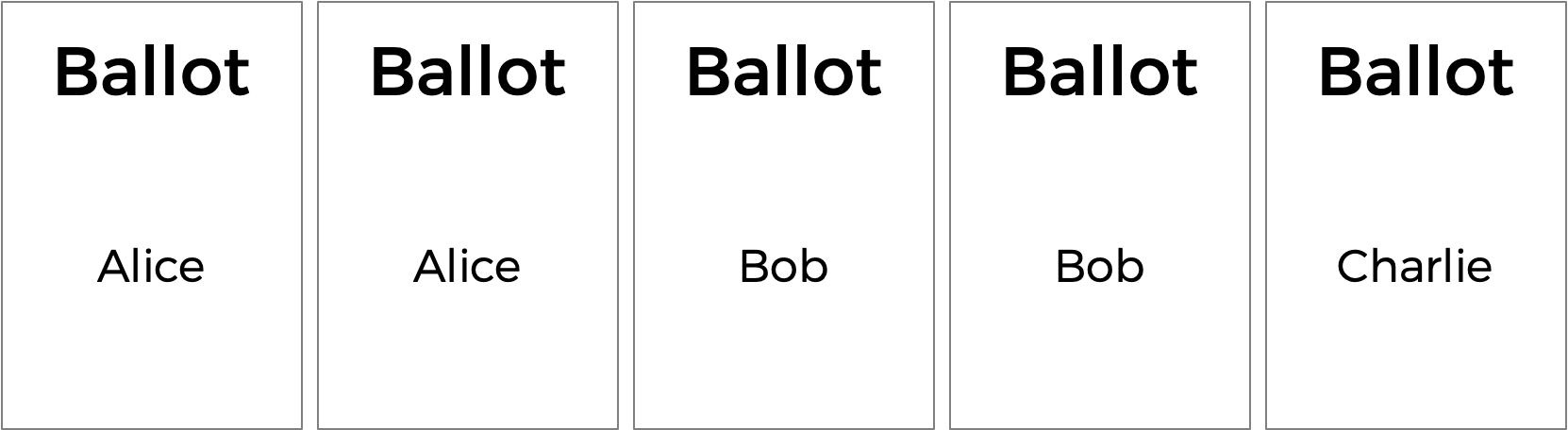
多数決では、AliceとBobはそれぞれ2つの票を持っているので引き分けとなります。しかし、それは正しい結果なのでしょうか?
別の種類の投票システムとして、順位選択制があります。順位選択制では、有権者は複数の候補者に投票することができます。トップの候補者に投票するだけでなく、優先順位に従って候補者をランク付けできます。したがって、投票結果は次のようになります。
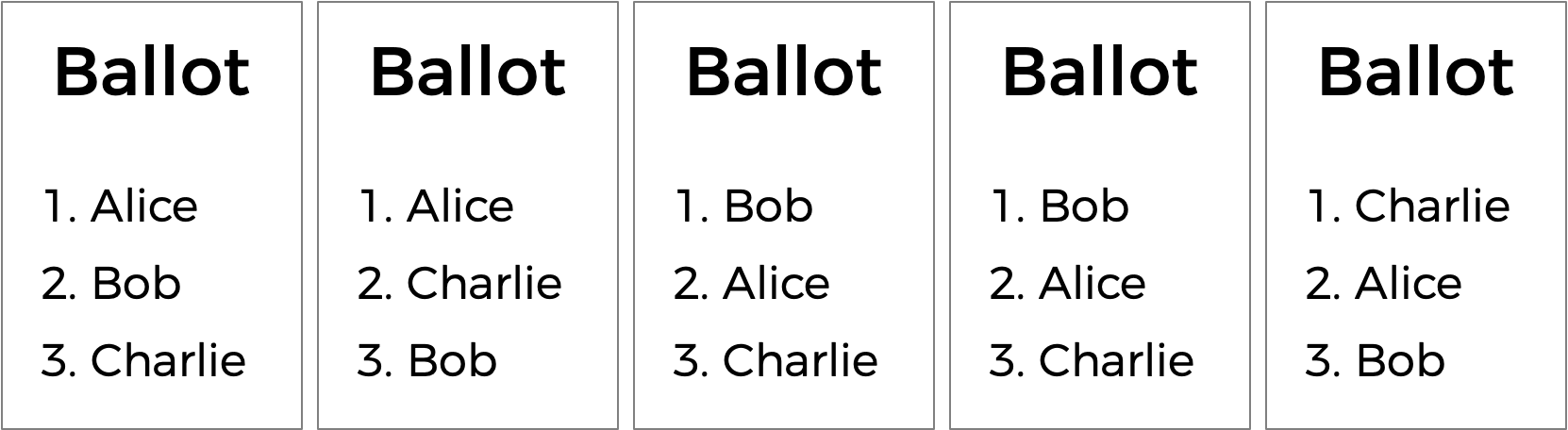
ここでは、各投票者は、第1候補を特定することに加え、第2および第3の候補も示しています。すると、以前は引分けだったのが、今では勝者が出る可能性があります。もともとAliceとBobが引き分けたので、Charlieは落選します。ですが、Charlieを選んだ有権者は、BobよりもAliceを選びました。ですので、ここではAliceが勝者と言えるでしょう。
順位選択制はまた、多数決のさらに別の潜在的な欠点を解決することができます。次の投票用紙を見てください。
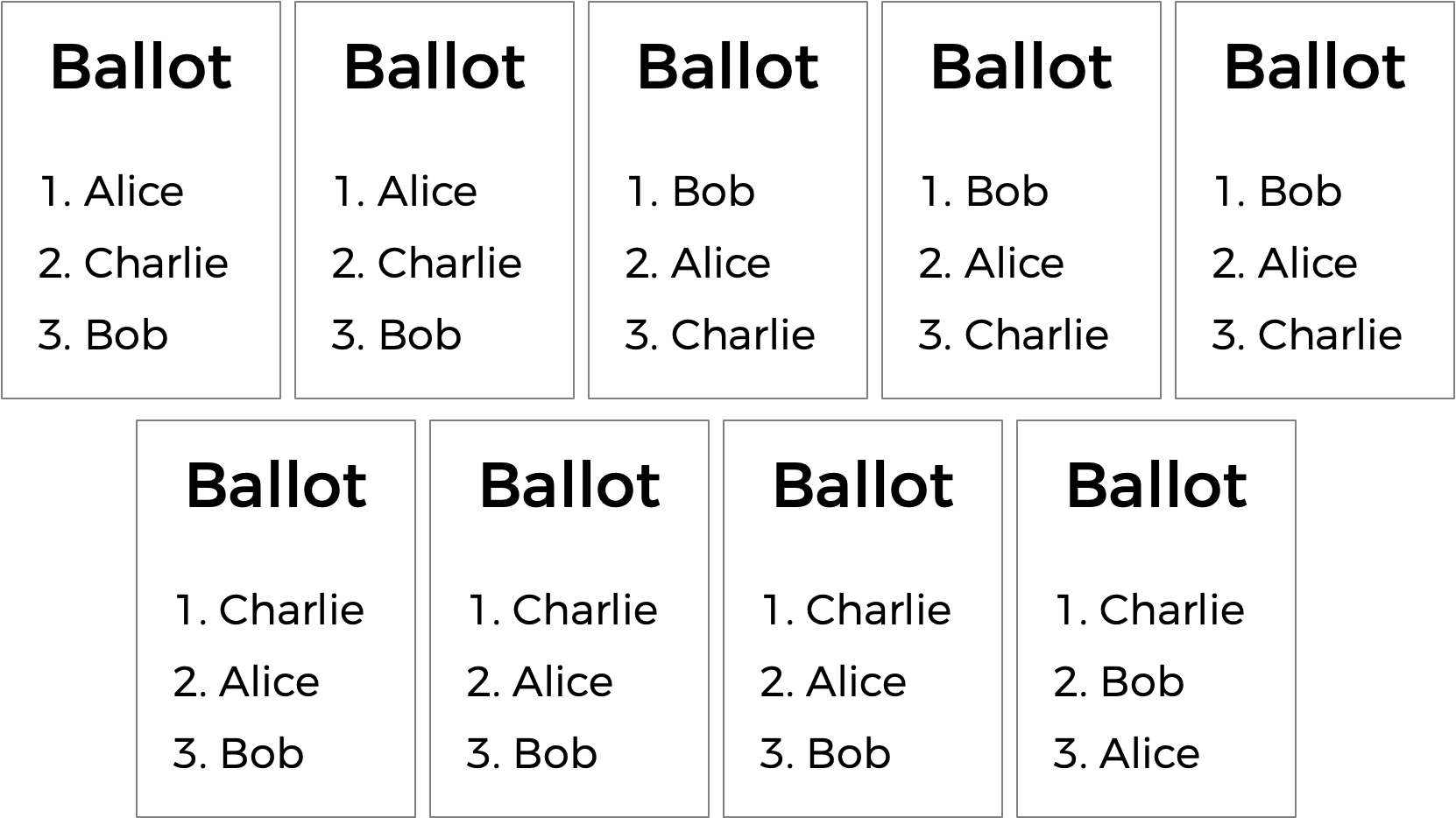
誰がこの選挙に勝つべきでしょうか。各投票者が第一候補のみを選択する多数決では、Charlieは4票でこの選挙に勝ち、Bobは3票、Aliceは2票です。(即時決選投票を知っている場合は、このシステムでもCharlieが当選します) 。ですが、しかし、AliceはCharlieではなく自分が選挙の勝者になるべきだという議論をするのは理にかなっているかもしれません、9人の投票者のうち、過半数 (5人) がCharlieよりもAlicを選んだのだから、ほとんどの人はCharlieよりもAliceが当選したほうが幸せでしょう。
この選挙でAliceは、いわゆる 「コンドルセ勝者」 です。Aliceは他の候補者と直接対決すれば勝利できたであろう人物です。もし選挙がAliceとBobだけだったら、あるいはAliceとCharlieだけだったら、Aliceが勝っていたでしょう。
Tideman投票方式 ( 「ranked pairs」 とも呼ばれます) は、ランク付けされた選択投票方式で、もし存在する場合は、コンドルセ勝者が選出されます。
一般的に、Tideman方式は、候補Aから候補Bへの矢印 (エッジ) が、候補Aが候補Bに対して直接対戦で勝つことを示す、候補の 「グラフ」 を構築することによって機能します。上の選挙のグラフは以下のようになります。
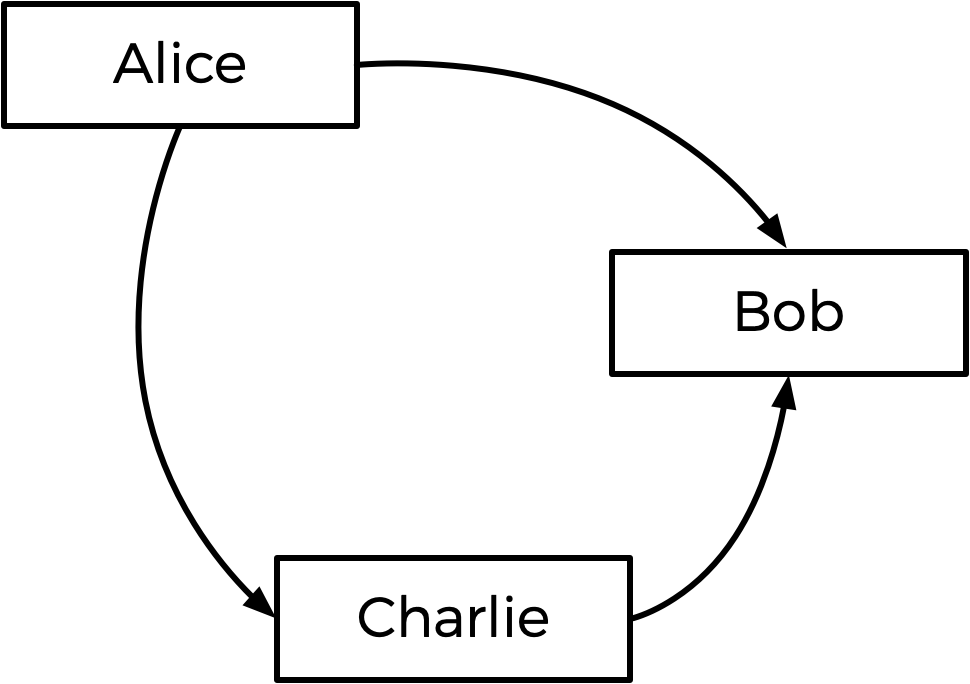
AliceからBobへの矢印は、より多くの有権者がBobよりもAliceを好むことを意味します (5人はAlic、4人はBobを好みます)。同様に、他の矢印は、より多くの有権者がCharlieよりもAliceを好み、より多くの有権者がBobよりもCharlieを好むことを意味します。
このグラフを見ると、Tideman方式は、選挙の勝者がグラフの開始点 (矢印で指されない候補者) であるべきだと言っています。この場合、開始点はAliceであり、Aliceだけが彼女を指す矢印を持っていないため、Aliceよりも直接好まれる相手はいません。よってAliceは、選挙の勝者と宣言されます。
ただし、矢印を描いてみると、コンドルセ勝者がいない可能性があります。以下の投票を考えてみましょう。

AliceとBobの間では、AliceがBobよりも7対2の差で好まれています。BobとCharlieの間では、BobのほうがCharlieより5対4の差で好まれています。しかしCharlieとAliceの間では、CharlieのほうがAliceよりも6対3の差で好まれています。グラフを描くと、開始点はありません!AliceがBobを破り、CharlieがAliceを負かします (ジャンケンのように) 。この場合、勝者を選ぶ方法はなさそうです。
これを処理するには、Tidemanアルゴリズムでは、候補者のグラフにサイクルが作成されないように注意する必要があります。どうするのでしょうか?アルゴリズムは、最も強いエッジを最初にロックします。これは、これらが最も重要であることはほぼ間違いないためです。特に、Tidemanアルゴリズムでは、対戦エッジは、勝利の 「強度」 に基づいて、一度に1つずつグラフに 「ロックイン」 されるように指定されます (相手よりも候補者を好む人が多ければ多いほど、勝利の確度は上がります)。サイクルを作成せずにエッジをグラフにロックできる限り、エッジが追加されます。それ以外の場合、エッジは無視されます。
上記の投票の場合、これはどのように機能しますか? 7人の投票者がBobよりもAliceを好むので (7人以上の投票者によって好まれる勝者が他にない) 、ペアとしての最大の勝利の余地は、AliceがBobを負かすことです。Alice-Bobの矢印が最初にグラフにロックされます。次に大きな差はCharlieがAliceに6-3で勝つことで、その矢印は次にロックされます。
次はBobのCharlieに対する5対4の勝利です。でも注意してほしいのは、今BobからCharlieに矢印をつければ、サイクルができるということです。グラフではサイクルを使用できないため、このエッジはスキップし、グラフには追加しません。考慮すべき矢印がもっとあれば、次の矢印を探しますが、これが最後の矢印なので、グラフは完成です。
この段階的なプロセスを以下に示し、最後のグラフを右に示します。
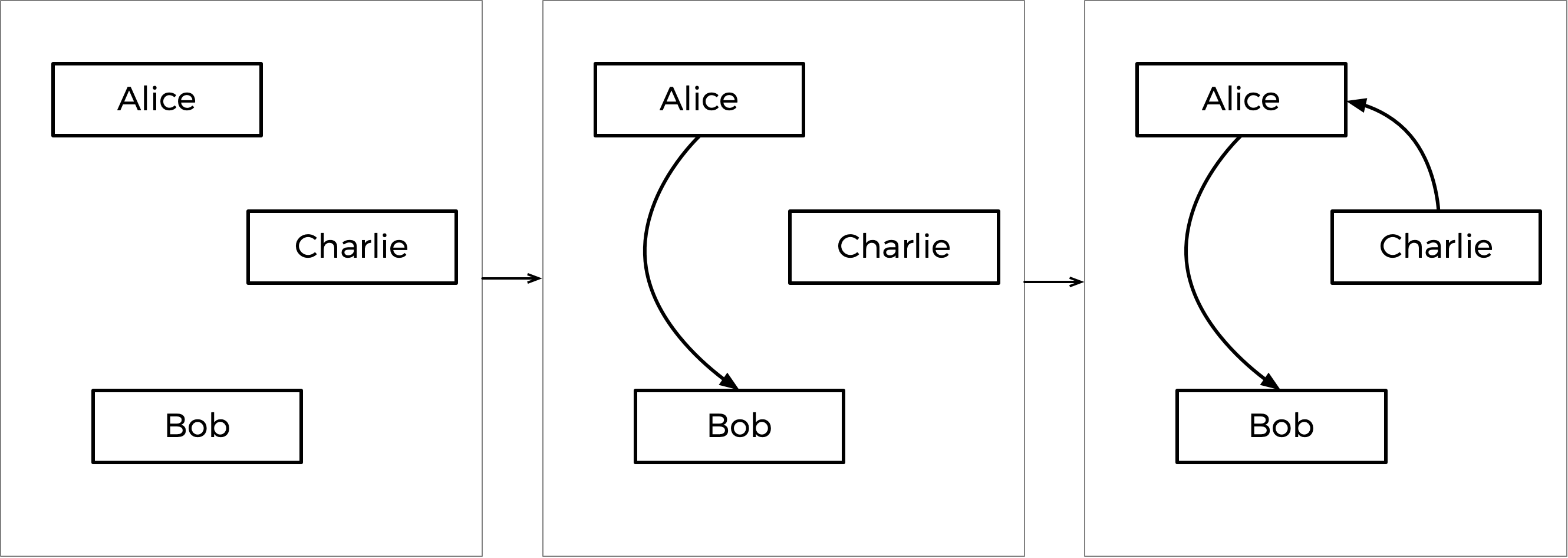
結果のグラフによると、Charlieがソース (Charlieを指す矢印はない) なので、Charlieがこの選挙の勝者であると宣言されます。
もっと正式に言えば、Tidemanの投票方法は3つの部分から構成されています。
- Tally: 有権者全員が自分たちの選好をすべて示したら、各候補者ペアについて、誰がどのくらいの票差で好まれるかを決定します。
- Sort: 候補者のペアを、勝利の強さの降順でソートします。勝利の強さは、優先候補者を好む投票者の数と定義されます。
- Lock: 最も強いペアから順番に候補のペアを調べ、そのペアをロックしてもグラフにサイクルが生じない限り、各ペアを候補グラフに 「ロックイン」 します。
グラフが完成したら、グラフの開始点 (エッジのないもの) が勝者になります。
始め方
ここでは、この問題の配布コード (スターターコード) をCS 50 IDEにダウンロードする方法を説明します。CS50 IDEにログインし、ターミナルウィンドウで次の各コマンドを実行します。
- すでに存在している
pset3ディレクトリに移動します。 mkdir tidemanを実行して、pset3ディレクトリにtidemanというディレクトリを作成 (新規作成) します。cd tidemanを実行して、そのディレクトリに移動 (ディレクトリを開く) します。wget https://cdn.cs50.net/2020/fall/psets/3/tideman/tideman.cを実行して、この問題の配布コードをダウンロードします。lsを実行します。この問題の配布コードはtideman.cというファイルにあります。
理解を深める
tideman.cを開いて、すでに存在するものを見てみましょう。
まず、2次元配列preferencesの設定に注目してください。整数preferences[i][j]は、候補者jより候補者iを好む投票者の数を表します。
このファイルには、候補者のグラフを表す2次元配列lockedも定義されています。lockedはboolean配列であり、locked[i][j]がtrueの場合は、候補iから候補jを指す矢印の存在を表します。falseはエッジがないことを意味します (興味があれば、グラフのこの表現は 「隣接行列」 として知られています) 。
次にpairと呼ばれる構造体structがあり、候補のペアを表すために使用されます。各ペアには、勝者winnerの候補者のインデックスと敗者loserの候補者のインデックスが含まれます。
候補者自体は、各候補の名前を表す文字列stringsの配列である配列candidatesに格納されます。また、配列pairsもあり、これは選挙の候補者のすべてのペア (どちらかが他方よりも優先される) を表します。
このプログラムには、2つのグローバル変数pair_countとcandidate_countもあり、それぞれ配列pairsとcandidatesの数を表します。
main関数に移ります。候補者の数を決定した後、プログラムはグラフlocked をループし、最初にすべての値をfalseに設定します。これは、最初のグラフには矢印がないことを意味します。
次に、プログラムは、すべての投票者をループ処理し、それらの優先順位をranks と呼ばれる配列に収集します (voteの呼び出しを介して) 。ここで、ranks[i]は、i番目の投票者の優先順位である候補者のインデックスです。これらのランクはrecord_preference関数に渡されます。この関数の役割は、これらのランクを取得してグローバル設定変数を更新することです。
すべての投票が完了すると、候補のペアはadd_pairsの呼び出しによって配列pairs に追加され、sort_pairsの呼び出しによってソートされ、lock_pairsの呼び出しによってグラフとしてロックされます。最後に、print_winnerが呼び出され、選挙の勝者の名前が出力されます。
ファイルのさらに下の方には、vote、record_preference、add_pairs、sort_pairs、lock_pairs、およびprint_winner関数が空白のままであることがわかります。あなたが作成するものです!
仕様
Tidemanの選挙をシミュレートするように、tideman.cの実装を完了します。
vote関数を実装します。- この関数は引数
rank、name、およびranksを取ります。nameが有効な候補者の名前と一致する場合は、配列ranksを更新して、有権者がその候補者を選好rankとして持つことを示す必要があります (ここで、0は最初の選好、1は2番目の選好などです)。
- ここでの
ranks[i]は、投票者のi番目の選好を表します。
- ランクが正常に記録された場合、この関数は
trueを返し、それ以外の場合 (例えば、nameが候補者の1人の名前ではない場合) はfalseを返します。
- 2人の候補者が同じ名前を持つことはないと想定できます。
- この関数は引数
record_preferences関数を実装します。- この関数は投票者ごとに1回呼び出され、引数として配列
ranks(ranks[i]は投票者のi番目の選好であり、ranks[0]は最初の選好であることを思い出してください) を取ります。
- この関数は、グローバル配列
preferencesを更新して現在の投票者の選好を追加します。preferences[i][j]は、候補jよりも候補iを好む投票者の数を表す必要があることを思い出してください。
- すべての投票者が各候補者をランク付けすると仮定します。
- この関数は投票者ごとに1回呼び出され、引数として配列
add_pairs関数を実装します。- この関数は、どの候補者が優先されているかについて、配列
pairsに、すべての候補者のペアを追加します。引き分けの (一方が他方より優先されない) 候補のペアは、配列に追加しないでください。
- この関数は、グローバル変数
pair_countを更新して、候補者のペアの数にする必要があります (したがって、ペアはすべてpairs[0]とpairs[pair_count - 1]の間に格納される必要があります)。
- この関数は、どの候補者が優先されているかについて、配列
sort_pairs関数を実装します。関数は、選択された候補者を好む投票者の数を勝利の強さとして定義し、勝利の強さの降順で配列pairsをソートします。複数のペアが同じ勝利の強さを持っている場合、順序はどちらでも良いと考えることができます。lock_pairs関数を実装します。- ロックされたグラフ
lockedを作成し、矢印がサイクルを作成しない限り、すべての矢印を勝利の強さの降順で追加します。
- ロックされたグラフ
print_winner関数を実装します。- この関数は、グラフの開始点である候補者の名前を出力します。複数の開始点が存在しないと想定することができます。
tideman.cでは、vote、record_preferences、add_pairs、sort_pairs、lock_pairs、およびprint_winner関数(必要に応じて、追加のヘッダファイルを含めます) の実装以外は変更しないでください。既存の関数の宣言を変更しない限り、tideman.cに関数を追加することができます。
ウォークスルー
使い方
プログラムは次の例のように動作します。
./tideman Alice Bob Charlie
Number of voters: 5
Rank 1: Alice
Rank 2: Charlie
Rank 3: Bob
Rank 1: Alice
Rank 2: Charlie
Rank 3: Bob
Rank 1: Bob
Rank 2: Charlie
Rank 3: Alice
Rank 1: Bob
Rank 2: Charlie
Rank 3: Alice
Rank 1: Charlie
Rank 2: Alice
Rank 3: Bob
Charlie
テスト
コードをテストして、以下の項目を処理できることを確認してください。
- 任意の数の候補者による選挙 (
MAXの9まで) - 候補者の氏名による投票
- 投票に参加していない候補者に対する無効な投票
- 当選者の印刷
check50を使用して以下を実行し、コードの正確さを評価してください。ただし、コンパイルとテストは必ず自分で行ってください。
check50 cs50/problems/2021/x/tideman以下を実行し、style50を使用してコードのスタイルを評価します。
style50 tideman.c提出方法
次のコマンドを実行し、GitHubのユーザー名とパスワードを入力してログインします。セキュリティのため、パスワードには実際の文字ではなくアスタリスク (*) が表示されます。
submit50 cs50/problems/2021/x/tideman