Notes – CS50 for Japanese: コンピュータサイエンスの入門

前回
検索
構造体
ソート
- 選択ソート
- バブルソート
再帰
マージソート

前回

私たちは、コード内の問題やバグを解決するツールについて学びました。特に、デバッガの使い方を発見しました。デバッガとは、プログラムの実行中にコードをゆっくりとステップ実行し、メモリ内の値を確認できるツールです。
もう1つの強力なツールは、技術的ではないにしても、ラバーダックのデバッグです。ラバーダックでは、ラバーダック (またはその他のオブジェクト) に何をしようとしているかを説明し、その過程で問題 (そして願わくば解決) を自分で認識します。
私たちはメモリを見て、グリッド内のバイトを視覚化し、各ボックス、つまりバイトに変数と配列を使って値を格納しました。

検索

配列を使用すると、コンピュータはすべての要素を一度に見ることはできません。コンピュータは配列を一度に1つずつしか見ることができませんが、その順序は任意です (Week 0を思い出してみましょう。Davidは、電話帳のページを1ページずつしか見ることができませんでした。順番にめくったり、もっと洗練されたやり方でめくったりしていました)。
検索は、特定の値を見つける問題を解決する方法です。単純なケースでは、値の配列の入力があり、特定の値が配列内にあるかどうかによって、出力はboolとなるでしょう。
今日は、検索のアルゴリズムについて見ていきます。これらについて説明するために、実行時間、つまり、一定のサイズの入力があった場合のアルゴリズムの実行にかかる時間を検討します。

Big O (ビッグO)

Week 0で、さまざまなタイプのアルゴリズムとその実行時間を紹介しました。

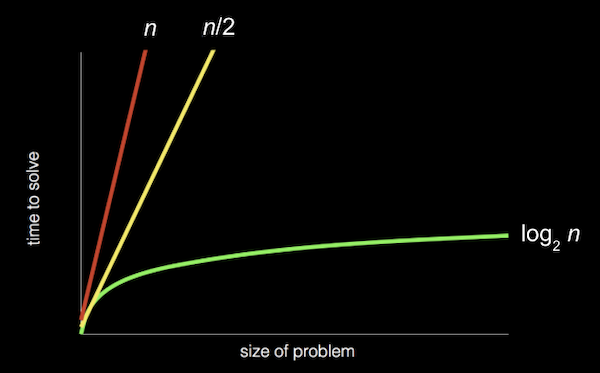
赤い線が一度に1ページずつ直線的に検索するということを思い出してください。黄色い線は一度に2ページを検索しているもので、緑の線は対数的に探索、つまり問題を半分ずつ分割するというものでした。
- これらの実行時間は、最悪の場合、つまり値の検出に最も時間がかかる場合です(最初のページではなく、最後のページに値がある場合)。

各実行時間を記述するより正式な方法として、ビッグO表記を使用することです。これは、「～のオーダー」と考えることができます。例えば、アルゴリズムが線形探索である場合、約O(n)ステップを要し、「ビッグOはn」または「nのオーダー」と読まれます。実は、一度に2つのページを見てn/2のステップをとるアルゴリズムもO(n)です。これは、nが大きくなるにつれて、支配的な要因、つまり最大項nだけが重要になるからです。上のグラフでは、縮小して軸の単位を変更すると、赤と黄色の線が非常に接近して表示されます。
対数実行時間は、底が何であってもO(log n) です。これは、nが非常に大きい場合は、実行時間としての近似値にすぎないからです。
一般的な実行時間は次のとおりです。
- O(n^2)
- O(n log n)
- O(n)
  - (一度に1ページずつ順番に検索する場合)
- O(log n)
  - (電話帳を毎回半分にする場合)
- O(1)
  - 問題の大きさに関係なく、一定数の手順を実行するアルゴリズムの場合

コンピュータ科学者はまた、我々のアルゴリズムのステップ数の下限であるビッグΩ (オメガ) 表記を使うかもしれません。Big Oは、ステップ数の上限、つまり最悪のケースです。
最も一般的なビッグΩの実行時間も似たようなものです。
- Ω(n^2)
- Ω(n log n)
- Ω(n)
- Ω(log n)
- Ω(1)
  - (電話帳で検索する場合。チェックする最初のページで探している名前が見つかるかもしれません)

線形探索、バイナリ検索(二分探索)

ステージ上にいくつかの仕掛けドアがあり、その後ろに数が隠されています。コンピュータは配列内の要素を一度に1つしか見ることができないため、同時に開くことができるドアも1つだけです。
たとえば、番号0を検索する場合は、一度に1つのドアを開く必要があり、ドアの後ろの番号について何も知らない場合は、最も単純なアルゴリズムは左から右に進むことです。
そこで、以下のような線形探索の擬似コードを書くことができます。

For i from 0 to n–1
    If number behind i'th door
        Return true
Return false

n個のドアそれぞれに0から n–1のラベルを付け、順番にチェックします。
- “Return false”はforループの外側にあります。なぜなら、すべてのドアの後ろを見た後にそれを実行したいからです。
- The big O running time for this algorithm would be O(n), and the lower bound, big Omega, would be Ω(1). このアルゴリズムのビッグOの実行時間はO(n) で、下限のビッグΩは Ω(1) です。

ドアの後ろの数字がソートされていることがわかれば、途中から始めて、探している値をより効率的に見つけることができます。
バイナリ検索の場合、アルゴリズムは次のようになります。

If no doors
    Return false
If number behind middle door
    Return true
Else if number < middle door
    Search left half
Else if number > middle door
    Search right half

バイナリ検索の上限はO(log n) で、下限は再びΩ(1) です (探している数値がちょうど検索を開始する中央にある場合) 。

64個の電球を使用すると、線形探索は、数ステップしか必要としないバイナリ検索よりもはるかに時間がかかることがわかります。
私たちは1ヘルツ (1秒あたりのサイクル) の周波数で電球を点滅させますが、プロセッサーの速度はギガヘルツ (1秒あたり数十億回の動作) で測定することができます。

コードを使用した検索

numbers.cを見てみましょう。

#include <cs50.h>
#include <stdio.h>

int main(void)
{
    int numbers[] = {4, 6, 8, 2, 7, 5, 0};

    for (int i = 0; i < 7; i++)
    {
        if (numbers[i] == 0)
        {
            printf("Found\n");
            return 0;
        }
    }
    printf("Not found\n");
    return 1;
}

ここでは、いくつかの値を中カッコで囲んで配列を初期化し、配列内の項目を1つずつチェックして、項目が0に等しいかどうかを確認します (もともとは仕掛けドアの裏を探していました) 。
- 値0が見つかった場合、 (成功を示す) 終了コード0を返します。それ以外の場合は、forループの後に1を返します (失敗を示します) 。
名前についても同じことができます。

#include <cs50.h>
#include <stdio.h>
#include <string.h>	

int main(void)
{
    string names[] = {"Bill", "Charlie", "Fred", "George", "Ginny", "Percy", "Ron"};

    for (int i = 0; i < 7; i++)
    {
        if (strcmp(names[i], "Ron") == 0)
        {
            printf("Found\n");
            return 0;
        }
    }
    printf("Not found\n");
    return 1;
}

names はソートされた文字列の配列であることに注意してください。
- 文字列は単純なデータ型ではなく、多くの文字の配列であるため、C言語では直接比較することはできません。幸いなことに、文字列ライブラリにはstrcmp (string compare) 関数があり、一度に1文字ずつ文字列を比較し、同じ場合は0を返します。
strcmp(names[i], "Ron") のみをチェックし、strcmp(names[i], "Ron") == 0とチェックしない場合、名前が見つからなくてもFoundと出力されます。これは、2つの文字列が一致しない場合、strcmpは0以外の値を返し、0以外の値は条件内でtrueに相当するためです。

構造体

電話帳を検索するプログラムを実装する場合は、名前と電話番号を含む「人 (person)」のデータ型が必要でしょう。
Cでは、次の構文でstructを使用して、独自のデータ型またはデータ構造を定義できることができます。

typedef struct
{
    string name;
    string number;
}
person;

プラス記号やハイフンなどの記号や書式を含めるため、数値numberには文字列stringを使用します。
- 構造体には他のデータ型が含まれています。
まず、構造体なしで電話帳を実装してみましょう。

#include <cs50.h>
#include <stdio.h>
#include <string.h>

int main(void)
{
    string names[] = {"Brian", "David"};
    string numbers[] = {"+1-617-495-1000", "+1-949-468-2750"};

    for (int i = 0; i < 2; i++)
    {
        if (strcmp(names[i], "David") == 0)
        {
            printf("Found %s\n", numbers[i]);
            return 0;
        }
    }
    printf("Not found\n");
    return 1;
}

namesの最初の名前がnumbersの最初の番号と一致するように注意する必要があります。
- 配列namesの特定のインデックスiにある名前が検索対象の名前と一致する場合、同じインデックスにある配列numbersの電話番号を返すことができます。
構造体を使用することで、プログラムに人為的なエラーが発生ないことをもう少し確信できます。

#include <cs50.h>
#include <stdio.h>
#include <string.h>

typedef struct
{
    string name;
    string number;
}
person;

int main(void)
{
    person people[2];

    people[0].name = "Brian";
    people[0].number = "+1-617-495-1000";

    people[1].name = "David";
    people[1].number = "+1-949-468-2750";

    for (int i = 0; i < 2; i++)
    {
        if (strcmp(people[i].name, "David") == 0)
        {
            printf("Found %s\n", people[i].number);
            return 0;
        }
    }
    printf("Not found\n");
    return 1;
}

構造型personの配列を作成し、peopleという名前を付けます (int numbers[]のように、他の変数と同じように、任意に名前を付けることができます)。person構造体内の各フィールドまたは変数の値は、ドット演算子.を使用して設定します。
- このループでは、同じperson構造体の番号numberが名前nameに対応していることがより確実になりました。
- const int NUMBER = 10;のような定数を使ってプログラムの設計を改善することもできます。コードではなく、別のファイルやデータベースに値を保存することを後で学びます。
近いうちに、構造体の定義を含む独自のヘッダファイルを作成し、プログラムのさまざまなファイルで共有できるようにします。

ソート

入力がソートされていない数値のリストである場合、ソートされたリストの出力を生成するために使用される多くのアルゴリズムがあります。ソートされたリストでは、すべての要素が順番に並んでいます。
ソートされたリストでは、効率のためにバイナリ検索を使用できますが、その効率のためのソートアルゴリズムを作成するには時間がかかる場合があります。そのため、コンピュータがアルゴリズムを実行するのにかかる時間と比べて、人間がプログラムを作成するのにかかる時間のトレードオフに直面することがあります。その他のトレードオフとしては、時間と複雑さ、または時間とメモリの使用量が考えられます。

選択ソート

Brianは舞台裏で、棚のソートされていない一連の数字を並べています。

6 3 8 5 2 7 4 1

いくつかの数値を取り出して適切な場所に移動することで、Brianは、それらの数値をすばやく並べ替えられます。
Brianはリストの各番号を順番に見ていき、これまで見た中で一番小さい番号を覚えています。彼は最後に到達すると、1が最小であることを理解し、それを最初に置く必要があることを知っているので、それを最初の番号6と入れ替えます。

6 3 8 5 2 7 4 1
–             –
1 3 8 5 2 7 4 6

次に、Brianは、少なくとも最初の数字が正しい位置にあることを知っているので、残りの数字の中から最小の数字を探し、それを次のソートされていない数字 (現在は2番目の数字) と交換することができます。

1 3 8 5 2 7 4 6
  –     –
1 2 8 5 3 7 4 6

8: そして、次に小さい数である3と8を入れ替えて、これを繰り返します。

1 2 8 5 3 7 4 6
    -   -
1 2 3 5 8 7 4 6

さらに何回かスワップすると、ソートされたリスト完成します。
このアルゴリズムは選択ソート (selection sort) と呼ばれ、擬似コードを使用してもう少し具体的にすることができます。

For i from 0 to n–1
    Find smallest item between i'th item and last item
    Swap smallest item with i'th item

ループの最初のステップは、リストのソートされていない部分の中で、i番目の項目と最後の項目の間にある最小の項目を探すことです。これは、i-1番目の項目までソートされたことがわかっているためです。
- 次に、最小のアイテムをi番目のアイテムと交換します。これにより、iでソートされたアイテムまですべてが構成されます。

選択ソートでアイテムがどのように移動してソートされるか、アニメーションを使用した視覚化を参照します。
このアルゴリズムでは、n個の要素すべてを調べて最小の要素を見つけ、n個のパスを作成してすべての要素をソートします。
より正式には、いくつかの数式を使用して、最大の要素が実際にはn^2であることを示すことができます。まず、n個の要素すべてを調べ、次にn-1、n-2の順に調べます。

n+(n–1)+(n–2)+…+1
n(n+1)/2
(n^2+n)/2
n^2/2+n/2
O(n^2)

n^2が最大の (支配的な) 要因であるため、アルゴリズムの実行時間はO (n^2) と言えます。

バブルソート

バブルソートと呼ばれる数値の組を繰り返し入れ替える、別のアルゴリズムを試すこともできます。
Brianは最初の2つの数字を見て、順番が合うように入れ替えます。

6 3 8 5 2 7 4 1
– –
3 6 8 5 2 7 4 1

次の6と8は順番に並んでいるので、交換する必要はありません。
次の8と5のペアをスワップする必要があります。

3 6 8 5 2 7 4 1
    – –
3 6 5 8 2 7 4 1

Brianはリストの最後に到達するまで続けます。

3 6 5 2 8 7 4 1
        – –
3 6 5 2 7 8 4 1
          – –
3 6 5 2 7 4 8 1
            – –
3 6 5 2 7 4 1 8
              -

リストはまだソートされていませんが、最大の値である8が右端に移動されているため、解には少し近づいています。他の大きな数字も右に移動して (バブルのように浮き上がって) います。
Brianは、リストをもう一度並べ替えます。

3 6 5 2 7 4 1 8
– –
3 6 5 2 7 4 1 8
  – –
3 5 6 2 7 4 1 8
    – –
3 5 2 6 7 4 1 8
      – –
3 5 2 6 7 4 1 8
        – –
3 5 2 6 4 7 1 8
          - –
3 5 2 6 4 1 7 8
            - -

3と6、また6と7を交換する必要はありませんでした。
- しかし、次に大きい値である7は、右に移動しました。

Brianはこのプロセスを何度か繰り返すことで、リストをソートする回数を増やすほど、完全にソートされたリストに近づいていきます。
選択ソートでは、パスごとに最小数をチェックするだけなので、ソートされたリストの最良のケースでも、最悪のケースと同じ数の手順を実行します。
バブルソートの擬似コードは次のようになります。

Repeat until sorted
    For i from 0 to n–2
        If i'th and i+1'th elements out of order
            Swap them

i番目の要素とi+1番目の要素を比較するので、iのn-2までの値を指定するだけです。次に、2つの要素が故障している場合は、それらを交換します。
- リストがソートされたらすぐに停止できます。スワップを行ったかどうかを覚えておけばよいからです。そうでない場合、リストはすでにソートされている必要があります。

バブルソートの実行時間を決定するために、ループ内にn-1の比較があり、最大でn-1のループがあるので、n^2-2n+2ステップの合計が得られます。しかし、最大の要因、つまり支配項は、nが大きくなるにつれて再びn^2になるので、バブルソートはO(n^2) を持つと言うことができます。基本的に選択ソートとバブルソートは実行時間の上限が同じであることがわかりました。
ここでの実行時間の下限は、すべての要素を一度見るとΩ(n) です。
したがって、これまで見てきた実行時間の上限は次のようになります。
- O(n^2)
  - 選択ソート、バブルソート
- O(n log n)
- O(n)
  - 線形探索
- O(log n)
  - バイナリ検索
- O(1)
下限の場合:
- Ω(n^2)
  - 選択ソート
- Ω(n log n)
- Ω(n)
  - バブルソート
- Ω(log n)
- Ω(1)
  - 線形探索、バイナリ検索

再帰

再帰とは、関数が自身を呼び出す機能です。これはまだコードでは確認していませんが、week 0に擬似コードで変換可能なものが見つかっています。

1  Pick up phone book
2  Open to middle of phone book
3  Look at page
4  If Smith is on page
5      Call Mike
6  Else if Smith is earlier in book
7      Open to middle of left half of book
8      Go back to line 3
9  Else if Smith is later in book
10     Open to middle of right half of book
11     Go back to line 3
12 Else
13     Quit

ここでは、ループのような命令を使用して特定の行に戻っています。
代わりに、残った本の半分にアルゴリズム全体を繰り返すことができます。

1  Pick up phone book
2  Open to middle of phone book
3  Look at page
4  If Smith is on page
5      Call Mike
6  Else if Smith is earlier in book
7      Search left half of book
8
9  Else if Smith is later in book
10     Search right half of book
11
12 Else
13     Quit

これは終わりのない循環プロセスのように見えますが、実際には関数への入力を変更し、問題を毎回半分に分割していますから、それ以上めくるページ数がなくなれば終了します。

Week 1でも、ブロックの「ピラミッド」を次のような形で実装しました。

#
##
###
####

高さ4のピラミッドは、高さ3のピラミッドに、さらに4つのブロックの列が追加されていることに注目してください。高さ3のピラミッドは高さ2のピラミッドに、3つのブロックの列が追加されています。高さ2のピラミッドは、高さ1のピラミッドに、2つのブロックの列が追加されます。最後に、高さ1のピラミッドは1つのブロックにすぎません。
この考え方を念頭に置いて、ピラミッドを描画する再帰関数を作成することができます。ピラミッドは、別の行を追加する前に、より小さなピラミッドを描画するために自身を呼び出す関数です。

マージソート

マージソートと呼ばれる別のアルゴリズムを使用して、ソートに再帰の概念を取り入れることができます。擬似コードは次のようになります。

If only one number
  Return
Else
    Sort left half of number
    Sort right half of number
    Merge sorted halves

実際には、2つのソートされたリストがあると考えられます。

3 5 6 8 | 1 2 4 7

2つのリストをマージして、各リストの先頭にある最小の要素を1つずつ取り出し、最終的なソート済みリストを作成します。

3 5 6 8 | _ 2 4 7

1

右側の1が1と3の間で一番小さいので、それからソートリストを始めましょう。

3 5 6 8 | _ _ 4 7

1 2

次に小さい2と3の数字は2なので、2を使います。

_ 5 6 8 | _ _ 4 7

1 2 3
_ 5 6 8 | _ _ _ 7

1 2 3 4
_ _ 6 8 | _ _ _ 7

1 2 3 4 5
_ _ _ 8 | _ _ _ 7

1 2 3 4 5 6
_ _ _ 8 | _ _ _ _

1 2 3 4 5 6 7
_ _ _ _ | _ _ _ _

1 2 3 4 5 6 7 8

これで完全にソートされたリストができました。
疑似コードの最後の行がどのように実装されるかを見てきましたが、今度はアルゴリズム全体がどのように動作するかを見ていきます。

If only one number
  Return
Else
    Sort left half of number
    Sort right half of number
    Merge sorted halves

ソートされていない別のリストから始めます。

6 3 8 5 2 7 4 1

まず、左半分をソートします。

6 3 8 5

それをソートするには、まず左半分をソートする必要があります。

6 3

これらの2つの半分には、それぞれ1つの項目しかないため、両方がソートされます。ソートされたリストの場合、これら2つのリストをマージします。

_ _ 8 5 2 7 4 1
3 6

左半分の右半分をソートし、マージします。

_ _ _ _ 2 7 4 1
3 6 5 8

左半分の両方が個別にソートされているので、ここでそれらをマージする必要があります。

_ _ _ _ 2 7 4 1
_ _ _ _
3 5 6 8

今やったことを右半分でやります。

_ _ _ _ _ _ _ _
_ _ _ _ 2 7 1 4
3 5 6 8

右半分の両方をソートします。

_ _ _ _ _ _ _ _
_ _ _ _ _ _ _ _
3 5 6 8 1 2 4 7

その後、ソートされた右半分のためにそれらをマージします。
最後に、2つのソート済みの半分があり、それらをマージして完全にソートされたリストを作成します。

_ _ _ _ _ _ _ _
_ _ _ _ _ _ _ _
_ _ _ _ _ _ _ _
1 2 3 4 5 6 7 8

各番号を1つの棚から別の棚に3回移動しました(リストが8、4、2、1に分割された後、再び2、4、8のソートされたリストにマージされたため)。そして、それぞれのシェルフでは、8つの番号を1つずつマージする必要がありました。
それぞれの棚はnステップを必要とし、必要なのはlog n個の棚だけなので、これらの係数を掛け合わせます。バイナリ検索の合計実行時間はO (log n) です。
- O(n^2)
  - 選択ソート、バブルソート
- O(n log n)
  - マージソート
- O(n)
  - 線形探索
- O(log n)
  - バイナリ検索
- O(1)
(log nが1より大きくnより小さいので、n log nはn (×1) とn^2の間にあります。)
最良の場合Ωでもn log nであることに変わりはありません。半分ずつ並べ替えてからマージする必要があるからです。
- Ω(n^2)
  - 選択ソート
- Ω(n log n)
  - マージソート
- Ω(n)
  - バブルソート
- Ω(log n)
- Ω(1)
  - 線形探索、バイナリ検索
マージソートは選択ソートやバブルソートよりも高速になる可能性がありますが、マージされたリストを各段階で一時的に保管するために、別の棚、つまりより多くのメモリが必要でした。より高速なソートのために、より高いコスト、つまりメモリ内の別の配列が必要であるというトレードオフに直面します。
最後に、もう1つの表記法であるΘ (シータ)があり、これを使用して、上限と下限が同じ場合のアルゴリズムの実行時間を記述します。たとえば、マージソートでは、最良の場合と最悪の場合の両方で同じステップ数が必要なため、Θ (n log n) が使用されます。そして選択ソートはΘ(n^2)です。:
- Θ(n2)
  - 選択ソート
- Θ(n log n)
  - マージソート
- Θ(n)
- Θ(log n)
- Θ(1)
大量のインプットを持つソートアルゴリズムの最終的な可視化を見てみましょう。