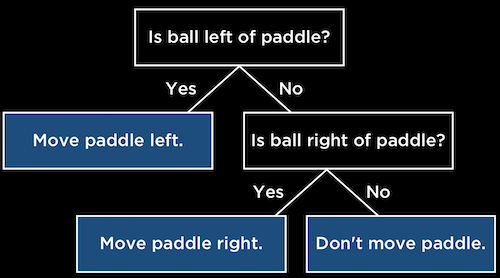
人工知能 (AI) とは、人間のように知的に、理性的に、あるいは人間が振る舞うようにコンピュータをプログラミングすることだと言えます。AIにはたとえば3目並べ (マルバツゲーム) などの、対戦相手の将来の手と、自分の最良の手を推論するゲームをプレイする能力が含まれるでしょう。 AIは、手書きのテキストを認識し、スパムメールを正確に検出し、ユーザの 「監視履歴」 に基づいてビデオを推薦し、さらには存在しない人間の画像を生成するかもしれません。 AIは単一のアルゴリズムや原理ではなく、問題解決のためのアプローチの集まりです。 ゲームで次に何をするか、電子メールがスパムかどうか、ユーザにビデオを推奨するかどうかなど、適切な意思決定 を下すようにコンピュータをトレーニングする必要があるでしょう。 パドルとボールを使ってブロックを壊すゲームを考えてみましょう。 コンピュータはボールが左に動いているのを検知できます。また、パドルを左に動かしてボールが地面に落ちる前にキャッチするようにコンピュータをプログラムできます。 意思決定ツリー を使用して、決定の背後にある論理を表すことができます。各ステップで質問が行われ、それぞれの回答に基づいてさらに質問または処理が行われます。 while game is ongoing:
if ball left of paddle:
move paddle left
else if ball right of paddle:
move paddle right
else:
don’t move paddle
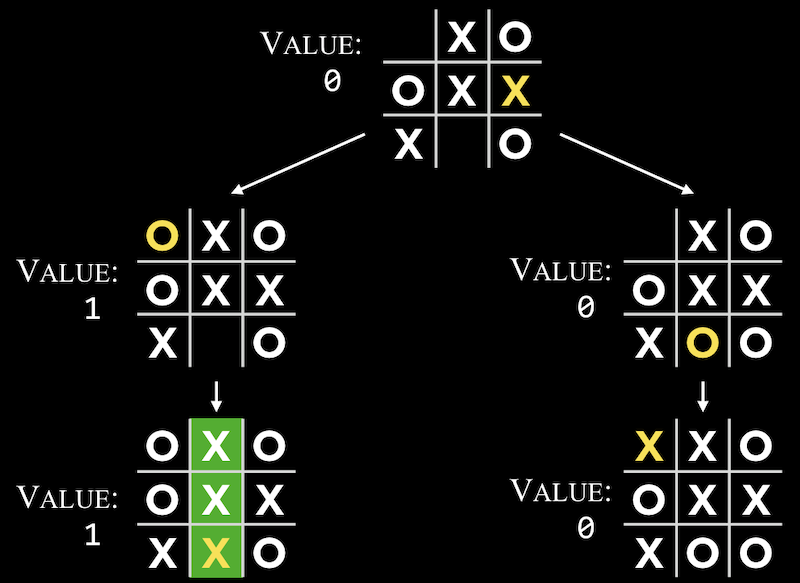
3目並べの場合、「現在の自分のターンで3つ並べられるか?」と考えるでしょう。もしそうなら、私たちはそのように選ぶべきです。そうでなければ、「対戦相手は次のターンで3つ並べられるか?」と考え、もしそうならそれを妨害するための手を考えます。しかし、どちらの条件も満たされていない場合、コンピュータをどのようにプログラムするかはまだ不明です。 これで、コンピュータが最適な決定をするために、より一般的なアルゴリズムを使用できることが分かりました。 ミニマックス は、すべての結果が値またはスコアを持ち、各プレイヤーがスコアを最大化または最小化しようとするゲームプレイのアルゴリズムです。たとえば、2人のプレイヤーXとOがいる3目並べでは、次の3つの可能性があります。Oのプレイヤーが勝つ場合、値-1を割り当てることができます。 Xのプレイヤーがつ場合、値1を割り当てることができます。 ここで、プレイヤーXは最終値を最大化し、プレイヤーOは最終値を最小化します。 終了していないゲームでも、各プレイヤーの最高の動きに基づいて値をつけることができます。たとえば、Xの番で、Xが勝てるゲームの値は1です。 もっと複雑なゲームでは、コンピュータはゲームツリー でそれぞれの可能性を考慮する必要があります。 Oの番なので、Oは2つのポジションのどちらかに移動でき、最後にXが移動します。ゲームが終了すると、可能な各動きと、その結果につながる動きにスコアを割り当てることができます。 ツリーが大きくなると、コンピュータはより多くの状態を表現し、可能なすべての動作を検討するでしょう。再帰的な擬似コードは次のようになります。 if player is X:
for all possible moves:
calculate score for board
choose move with highest score
else:
for all possible moves:
calculate score for board
choose move with lowest score
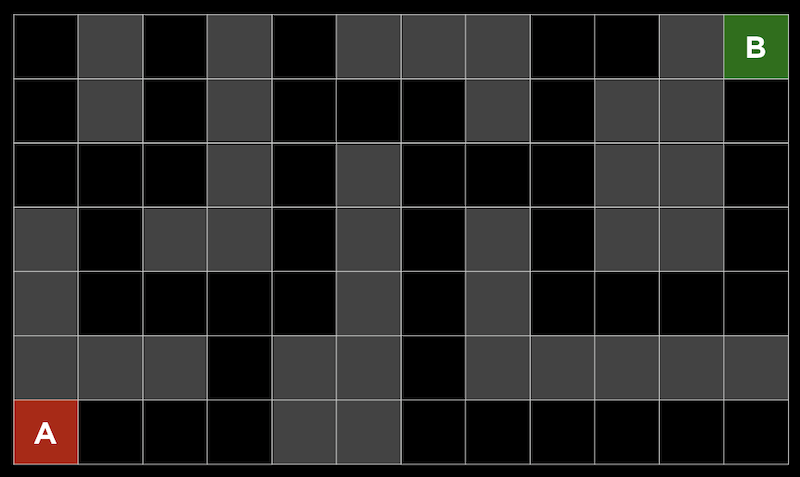
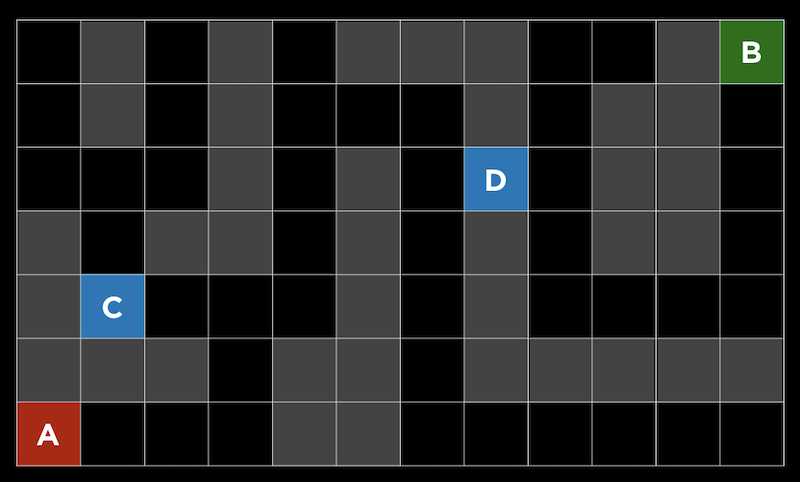
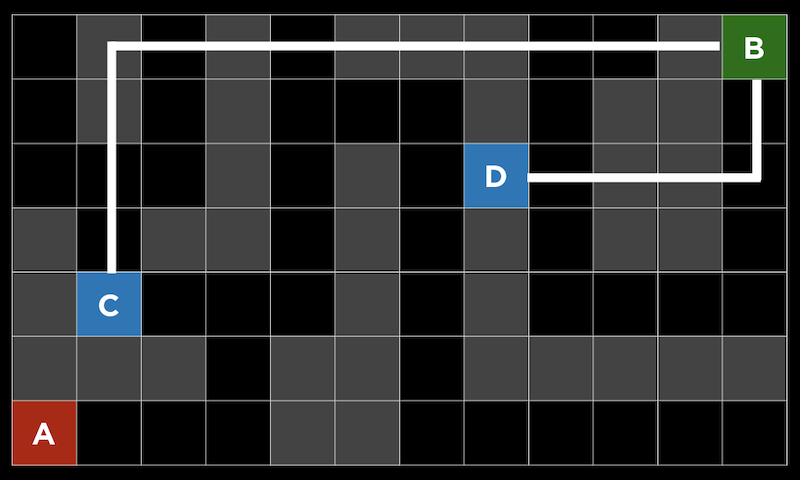
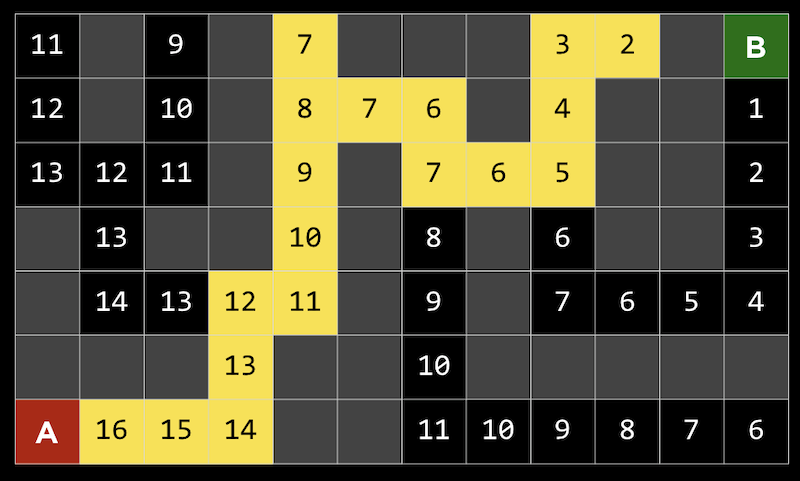
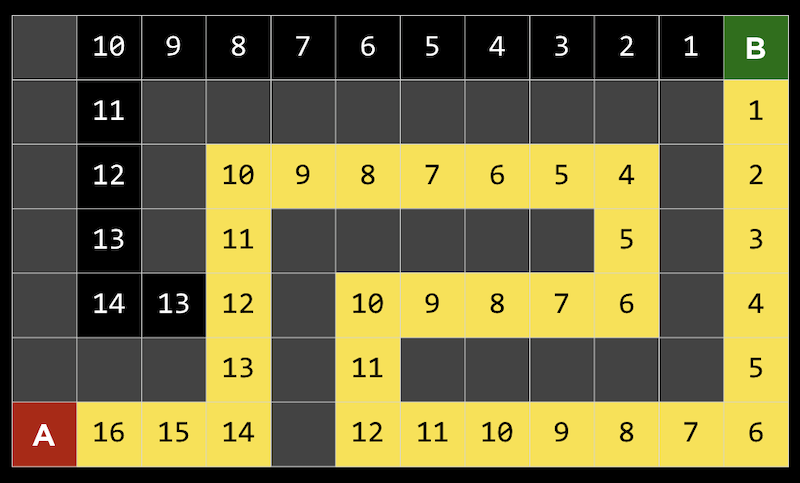
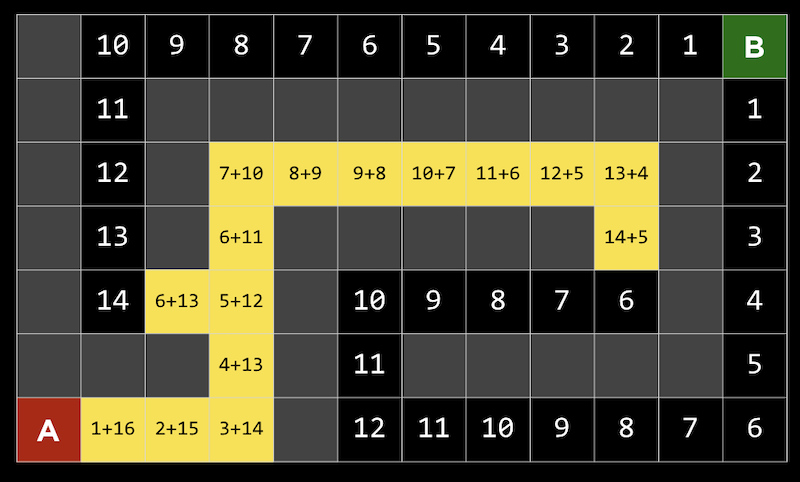
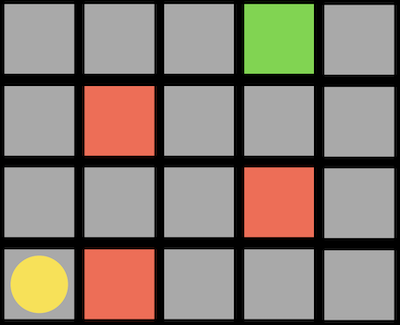
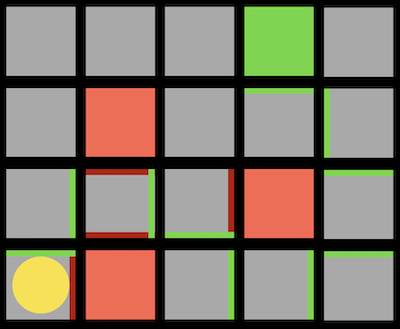
このアプローチの1つの問題は、ゲームで計算するには動きが多すぎる可能性があることです。3目並べには255,168種類の組み合わせしかありませんが、チェスでは最初の4手でも2880億の組み合わせがあります。すべての手を考慮すると、可能なゲームの下限はおよそ1029000 です。 追跡する経路や分岐を制限することにより、ミニマックスアルゴリズムを改善できます。深さ制限ミニマックス では、評価関数 を用いて限られた数の動きに対する期待値を推定するので、アルゴリズムは妥当な時間で判断を下すことができます。 ミニマックスアルゴリズムは一種の探索アルゴリズム であり、目標はゲームにおける次の動きまたはある問題の解を見つけることです。 問題の例としては、迷路を通り抜ける道を見つけることや、地図を与えられたとして現実世界の2つの場所を結ぶ経路を見つけることが考えられます。 A点からB点へ移動する迷路を考えることができます。灰色の四角は壁を示し、黒い四角は通路を示します。 深さ優先探索 という戦略は、可能性のある経路をたどり、選択が必要な場合にはランダムに選択し、それ以上の選択が不可能な場合にのみ逆方向に進むというものです。迷路では、最初の分岐点が見つかるまで道を進み、他に情報がないのでランダムに左を選び、行き止まりに到達するまで続けることができます。次に、前の分岐点に戻り、別のルートをたどります。これは目標に達するまで繰り返されます。 このアルゴリズムの1つの問題は、最初に戻って別の方向に進む前に領域内のすべてのパスを考慮するため、時間がかかりすぎることです。もう1つの問題は、ランダムな選択によってパスが長くなる可能性があるため、検出されたルートが最も効率的ではない可能性があることです。 幅優先探索 は、各パスを一度に1ステップずつ取っていくアルゴリズムで、出発点から外側を探索するようなものです。これにより、最短のパスを見つけることができますが、不必要なパスも数多く探索できます。これらのアルゴリズムはどちらもアンインフォームド・サーチ に分類されており、アルゴリズムは問題に関する追加情報を持っていません。 インフォームド・サーチ では、問題に関する知識を用いて、解を推定するヒューリスティクス を用いてより効率的に解を見つけます。たとえば、この迷路では、BとDの間の距離がCとDの間の距離よりも近いと 「思われる」 ので、正方形Dは正方形Cよりも優れていると推定できます。 迷路では、このヒューリスティックはマンハッタン距離 と呼ばれ、2つの正方形の間の壁を無視して、垂直方向と水平方向の正方形の数を数えることができます。 この追加情報を使って、各分岐点でより良い選択をすることができます。 貪欲な最良優先探索 は、道路の分岐点ごとに、最良の値を持つパスを選びます。この場合、マンハッタン距離で最も小さい距離になります。距離は任意の正方形に対して簡単に計算できるため、各正方形にラベルを付けることができます。ここで、アルゴリズムが各分岐で最適な値へのパスを取ることがわかります。8の値を持つ正方形では、両方の可能性が7の値を持っていたので、左のパスを取り、それが行き止まりだったので、他のパスに戻りました。しかし最後には壁に達しました。したがって、逆方向に進み、次の分岐の値を5にして、最終的にゴールに到達します。アルゴリズムは各正方形に到達した時点でヒューリスティックを計算するだけですが、視覚化しやすいようにすべての正方形にラベルを付けました。 しかし、このアルゴリズムでさえ、最も効率的なパスを見つけられないかもしれません。なぜなら、最初は非効率的なパスが良い選択のように見えるかもしれないからです。 ここでは、最初の分岐で左または上に移動できますが、ゴールが右上にあっても、左へのパスが実際には短くなります。 A*検索 ( 「Aスター検索」 と発音します) では、パスのヒューリスティック値と、そのパスですでに移動した距離の両方が使用されます。上記の例で、各ステップでその値を計算できます。 例えば最初のステップでは、一歩踏み出してみると、ゴールからマンハッタンまでの距離が16の正方形にあるので、合計値は1+16になります。これを繰り返しますが、最終的には、15歩進んだところでゴールから6歩離れているか (右端) 、13歩進んだところでゴールから6歩離れているか (左端) のどちらかであることがわかります。より効率的なソリューションを実現するには、左の方向に進む必要があります。 A*探索は、正確なヒューリスティックがあれば最適です。理論的には、ヒューリスティックは計算が迅速であるため、検索全体が効率的になります。 機械学習 の一種で、コンピュータがその経験から学習することができるものは強化学習 と呼ばれ、各ステップでの行動が肯定的か否定的かをコンピュータは学習できます。たとえば、プレイヤーがゴールに移動しなければならないゲームで、 (プレイヤーには見えない) 障害物に遭遇した場合、ゲームは終了します。 ここでは、プレイヤーは黄色の円で、マップ内には赤い障害物があり、そして緑色のブロックに移動しようとしています。 各ステップの後、コンピュータは安全に移動できる方向と、そうでない方向を学習します。 赤い線はコンピュータが回避するように学習した方向を示し、緑の線は学習した方向が安全であることを示します。 このゲームが十分に試行されていれば、コンピュータはどの順番でゴールに向かえばいいかを把握しているでしょう。 このアルゴリズムは最適なパスを見つけるのにも非効率的であることがわかるので、探索する (新しいアクションを試す) のと利用する (その前に実行した行動を安全に使用する) の両方を行いたいと考えています。 この2つはランダムに行われます。 epsilon = 0.10
if random() < epsilon:
make a random move
else:
make the move with the highest valueこの場合は10%として、ある程度の確率で、このアルゴリズムは以前に試した行動を繰り返すか、新たな行動を試します。 ここでは、パンケーキをひっくり返す方法を学習するロボットの例を見てみましょう。パンケーキをひっくり返す試みは何度も失敗しますが、最後にはパンを動かす方法を見つけました。 もう一つのアプローチは自然から触発されたもの、つまり最も適合する生物が時間とともに生存し進化するという考え方です。遺伝的アルゴリズム では、問題を解くために多くのアルゴリズムが作られますが、たとえうまくいかなくても、最良のアルゴリズムは、十分に優れたアルゴリズムが得られるまで、変異されるか、ランダムに変化します。 擬似コードは次のようになります。 make initial generation of candidates randomly
repeat until successful:
for each candidate:
calculate candidate's fitness
remove least fit candidates
make new generation from remaining candidates
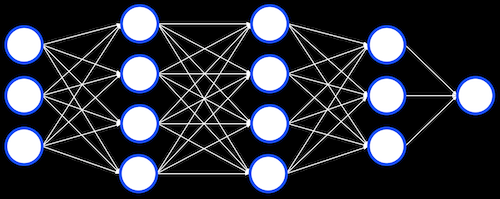
地図上での車のシミュレーションの例を見てみましょう。車の多くはすぐに壁に衝突しますが、壁を避けるためにセンサーを使っている車もあります。そして最高の候補や、最も遠くまで走った候補に、何世代にもわたってランダムな変更を施すことで、衝突せずに遠くまで行ける車ができます。 これらのアルゴリズムは、いくつかのボトルネック、または局所的な最大値に達する可能性があり、その場合はランダムな突然変異によって改善することができなくなります。他の完全に異なるアルゴリズムのみで改善することができます。 このアルゴリズムの他の応用例は、ビデオ・レコメンドであり、ここでは、視聴されたビデオを強化学習として考えることができます。 人間の脳では、ニューロン同士が信号をやり取りして計算を行います。ニューラルネットワーク はニューロンの集まりであり、デジタルにシミュレーションすることもできます。いくつかのニューロンあるいはユニット では、ある値を保存し、それを渡す前に計算を行うことができます。 ユニットのレイヤーを持つこともできます。各ユニットは、出力を次のユニットに渡す前に、入力に対して何らかの計算を実行します。 ディープラーニング とは、こうしたニューラルネットワークを線形代数と組み合わせて、ある問題を解決することです。十分な入力データが与えられれば、これらのニューラルネットワークを訓練して、入力を出力に変換するための値と計算を設定することができます。アプリケーションの例は手書き認識です。手書き数字の多くの画像に実際の値をラベリングし、ニューラルネットワークを訓練して新しい画像を認識させることができます。 同様に、電子メールが正当なものかスパムかのラベルを付けることができ、ニューラルネットワークは新しい電子メールをどのカテゴリに入れるかを判断することができます。 これらのアルゴリズムのポイントは大量のデータであり、それによりニューラルネットワークはより正確になり得ます。 人間の画像もニューラルネットワークで生成できます。最初は、少数のピクセルしか生成できないでしょうが、その画像を入力として、より人間の画像に近いディテールを加えることができ、最終的には納得のいく画像を生成することができるでしょう。 機械学習に関する懸念の1つは解釈可能性 ( interpretability ) で、ニューラルネットワークが出力をするために何をしているのかを人間が理解することが難しいというものです。